Kurzzusammenfassung
Die im Winter beobachtete gesteigerte Sterblichkeit in gemäßigten Zonen wird zu großen Teilen der saisonalen Influenza zugeschrieben. Eine kürzlich erfolgte Reanalyse von Laborexperimenten deutet darauf hin, dass die absolute Luftfeuchtigkeit einen stark modulierenden Einfluss auf das Überleben des Influenzavirus in der Luft und dessen Übertragung ausübt. Hier übertragen wir diese Ergebnisse auf die menschliche Bevölkerung und zeigen, dass das Auftreten einer gesteigerten, auf Influenza basierenden Sterblichkeit zur Winterzeit in den USA mit ungewöhnlich niedrigen Werten absoluter Luftfeuchtigkeit in den vorangehenden Wochen in Zusammenhang steht.
Wir verwenden dann ein epidemiologisches Modell, in welchem beobachtete absolute Feuchtigkeitsbedingungen die Übertragungsraten von Influenza modulieren, und simulieren erfolgreich den saisonalen Verlauf der mit Influenza verbundenen Sterblichkeit. Die Modellergebnisse deuten darauf hin, dass allein die unmittelbare Modulation der Übertragungsfähigkeit von Influenza durch die absolute Luftfeuchtigkeit ausreichend ist, um diese beobachtete Saisonalität hervorzurufen. Diese Erkenntnisse bieten eine epidemiologische Untermauerung der Hypothese, dass die absolute Luftfeuchtigkeit für die saisonalen Variationen der Influenzaübertragung in gemäßigten Zonen verantwortlich ist.
Zusammenfassung der Autoren
Die Ursache für die Saisonabhängigkeit der Übertragung von Influenza ist von hoher Bedeutung für die öffentliche Gesundheit und gleichzeitig von grundlegendem wissenschaftlichen Interesse. Hier präsentieren wir statistische Analysen sowie ein mathematisches Modell der Übertragung epidemischer Influenza und liefern damit fundierte epidemiologische Belege für die Hypothese, dass die absolute Luftfeuchtigkeit (a. F.) die Saisonabhängigkeit der Influenza-Übertragung in gemäßigten Zonen bedingt. Wir zeigen, dass über die USA hinweg das Auftreten einzelner Influenza-Epidemien im Winter mit ungewöhnlich niedrigen Bedingungen der absoluten Feuchte in Verbindung steht.
Zusätzlich verwenden wir die a. F. zur Modellierung der Basisreproduktionszahl von Influenza in einem mathematischen Modell der Influenza-Übertragung und vergleichen diese Simulationen mit beobachteten übermäßigen Sterblichkeitsraten durch Pneumonie und Influenza. Diese Simulationen erfassen wesentliche Details des in den gesamten USA beobachteten saisonalen Verlaufs der Influenza. Die Ergebnisse deuten darauf hin, dass die a. F. sowohl die Saisonalität des Auftretens von Influenza als auch den Zeitpunkt einzelner Influenza-Ausbrüche zur Winterzeit in gemäßigten Zonen beeinflusst. Der Zusammenhang zwischen ungewöhnlich niedrigen Bedingungen absoluter Feuchte und dem Ausbrechen von Influenza zur Winterzeit zeigt, dass es möglich sein könnte, auf kurze Sicht leistungsfähige probabilistische Vorhersagen von Influenza-Epidemien zu entwickeln.
Studie von Jeffrey Shaman1*, Virginia E. Pitzer2,3,4, Cécile Viboud2, Bryan T. Grenfell2,4,5, Marc Lipsitch6,7,8
In gemäßigten Zonen sind Influenza-Epidemien zur Winterzeit für eine erhebliche Morbidität und Sterblichkeit verantwortlich [1]. Die saisonalen Epidemien treten immer wieder auf, da das Influenzavirus durch Antigendrift der Oberflächenantigene in der Lage ist, die menschliche Immunantwort zu umgehen [2]. Jüngere Influenza-Epidemien waren auf die gleichzeitige Verbreitung dreier Virus-(Sub-)Typen, A/H1N1, A/H3N2 und B, zurückzuführen, von denen im Allgemeinen in einem bestimmten Winter jeweils einer lokal vorherrschte [3–5]. In den seltenen Fällen, in denen ein neues Virus, gegen das Menschen kaum oder nicht immun sind, von Vögeln oder anderen Säugetieren als Wirte auf den Menschen übergeht, kann eine Influenza pandemischen Ausmaßes ganzjährig, also auch in den Frühlings- und Sommermonaten, auftreten. Ein Beispiel ist die aktuelle H1N1v-Pandemie [6–9]. Trotz zahlreicher Berichte, die die in der Wintersaison vorherrschende Übertragung epidemischer Influenza in gemäßigten Zonen beschreiben [10], ist unser Verständnis der dieser Saisonabhängigkeit zugrundeliegenden Mechanismen noch sehr begrenzt.
Experimentelle Studien legen nahe, dass das Überleben des Influenzavirus in aerosolisierten Tröpfchen stark mit der absoluten Feuchtigkeit der Umgebungsluft verbunden ist, in der Weise, dass die Überlebensfähigkeit der Viren mit abnehmender a. F. steigt [11]. In Laborexperimenten an Meerschweinchen wurde eine vergleichbare Beziehung zwischen absoluter Feuchte und der Übertragung luftgetragener Influenzaviren beobachtet; die Übertragungsrate stieg mit abnehmendem absolutem Feuchte-Niveau merklich an (Abbildung 1).
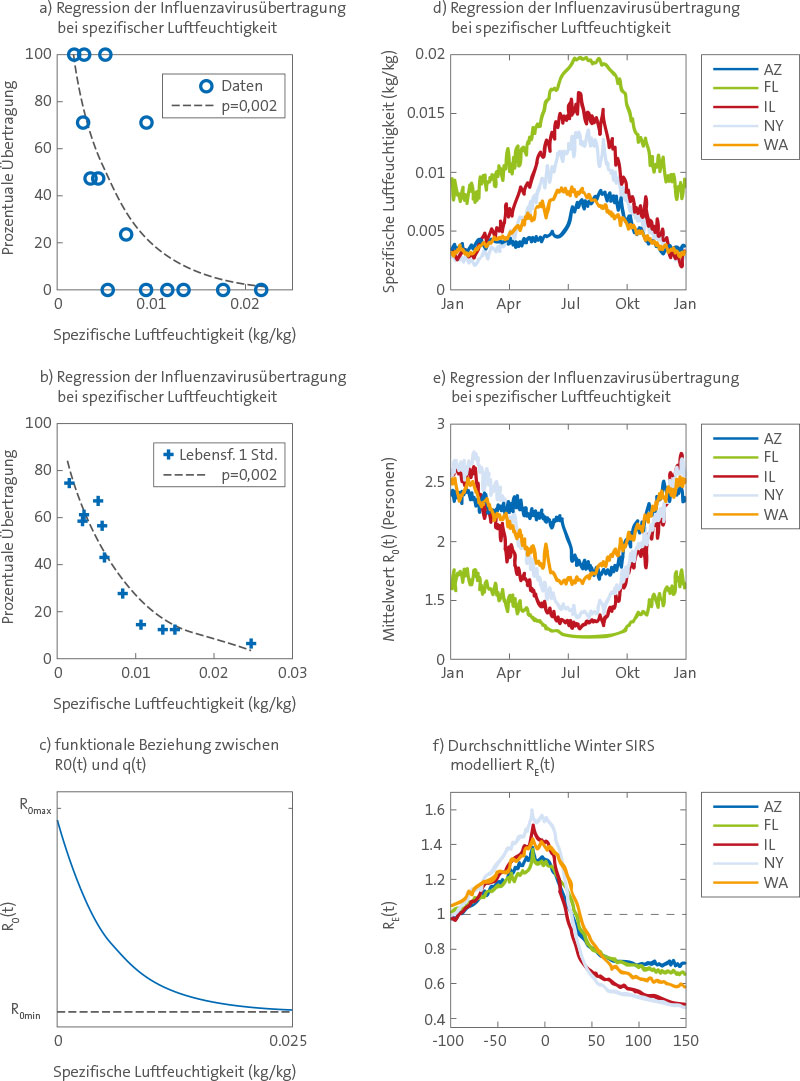
Analysen von Labordaten, Umweltdaten und SIRS-Modellsimulationen (A) Log-lineare Regression von Daten zur Übertragung luftgetragener Influenzaviren zwischen Meerschweinchen [14,15] auf die spezifische Luftfeuchtigkeit (ein Maß der a. F.); (B) log-lineare Regression von 1-h-Überlebensraten von Influenzaviren [28] auf die spezifische Luftfeuchtigkeit; (C) funktionale Beziehung zwischen R0(t) und q(t) gemäß Gleichung 4; (D) tägliche Klimatologie der Reanalyse der spezifischen Luftfeuchtigkeit 2 m über dem Boden von 1972–2002 durch die NCEP-NCAR [23] für Arizona, Florida, Illinois, New York State und Washington State; (E) tägliche Durchschnittswerte für R0(t) von 1972–2002, abgeleitet aus den Klimadaten zur spezifischen Luftfeuchtigkeit unter Verwendung der Best-Fit-Parameterkombination aus SIRS-Simulationen (R0max = 3,52; R0min = 1,12) und die funktionale Form (Abbildung 1C und Gleichung 4); (F) durchschnittliche RE(t) für alle Ausbrüche zur Winterzeit in den zehn Best-Fit-Simulationen in jedem Staat, von 100 Tagen vor bis 150 Tage nach Beginn des Ausbruchs (mindestens 400 Infektionen/Tag in den zwei Wochen davor; mindestens 5000 Infektionen/Tag an mindestens 1 Tag in den darauffolgenden 30 Tagen). Abbildung 1A und 1B sind Neuzeichnungen nach Shaman und Kohn [11] unter Verwendung der spezifischen Luftfeuchtigkeit als Maß der absoluten Feuchte. doi:10.1371/journal.pbio.1000316.g001
Ergebnisse
Absolute Feuchte und der Ausbruch von Influenza zur Winterzeit
In den gemäßigten Zonen der Welt ist die absolute Feuchte im Winter am geringsten und im Sommer am höchsten (Abbildung 1D). Dieser saisonale Zyklus begünstigt eine Zunahme sowohl des Überlebens als auch der Übertragung von Influenzaviren zur Winterzeit und kann möglicherweise den beobachteten saisonalen Höhepunkt der Morbidität und Sterblichkeit durch Influenza im Winter erklären. Aus Langzeiterfassungen der übermäßigen Sterblichkeit an Pneumonie und Influenza (P&I) in den USA, die einen robusten Indikator für das zeitliche Auftreten und die Auswirkungen von Epidemien auf nationaler und lokaler Ebene darstellen, ist klar ersichtlich, dass jährlich zur Winterzeit die Sterblichkeit einen Höhepunkt erreicht [4] (Abbildung S1).
Hier erarbeiten wir eine epidemiologische Untermauerung dieser bislang laborgebundenen Erkenntnisse, die implizieren, dass die absolute Feuchte maßgeblich für die saisonale Übertragung von Influenza verantwortlich ist. Zunächst analysieren wir dazu die räumliche und zeitliche Variation des Auftretens von Influenza-Epidemien für die kontinentalen USA zwischen 1972 und 2002 und korrelieren diese beobachtete Variabilität mit Aufzeichnungen der absoluten Feuchte für die gleichen Zeiträume und Standorte. Dann zeigen wir auf, dass ein mathematisches Modell der Influenza-Übertragung in den USA die räumliche und zeitliche Variation epidemischer Influenza wiedergeben kann, wenn die täglichen Bedingungen absoluter Feuchte innerhalb jedes Staates verwendet werden, um die Basisreproduktionszahl, R0(t), des Influenzavirus zu modulieren.
Unsere erste Überprüfung der Hypothese, dass eine niedrige absolute Feuchte die gesteigerte Übertragung von Influenza zur Winterzeit maßgeblich fördert, besteht in der Untersuchung, ob der Ausbruch der Influenza-Epidemie jeden Winter – dessen Zeitpunkt mit den Jahren beträchtlich variiert (Abbildung S1) – mit einem vorangegangenen Zeitraum ungewöhnlicher niedriger absoluter Feuchte einhergeht. Wir definieren den Ausbruch der Influenza zur Winterzeit als das Datum, an dem die zur Winterzeit beobachtete übermäßige P&I-Sterblichkeit für zwei aufeinanderfolgende Wochen einen festgelegten Schwellenwert erreicht oder überschritten hat (z. B. 0,01 Todesfälle/100.000 Personen/Tag). Dieses Ausbruchsdatum wurde für jeden der 30 Winter des Beobachtungszeitraums 1972–2002 in allen 48 zusammenhängenden Staaten und dem District of Columbia (DC) separat ermittelt. Anschließend haben wir die anormalen Bedingungen absoluter Feuchte (a. F.‘) vor und nach diesen Ausbruchsdaten untersucht. A. F.′ ist die lokale tägliche Abweichung der absoluten Feuchte von ihrem 31-jährigen Mittel für jeden Tag (wie in Abbildung 1D für fünf Staaten dargestellt), definiert als:
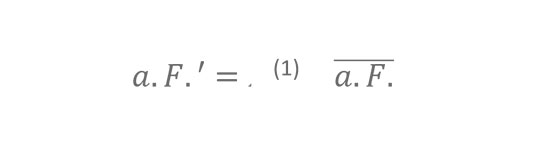
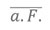 ) den täglichen Durchschnittswert von 1972–2002 repräsentiert. In niedrigen Breiten wie den USA ist das absolute Feuchte-Niveau im Winter ohnehin schon wesentlich niedriger als im Sommer (Abbildung 1D). Unter Zuhilfenahme von a. F.′ können wir ermitteln, ob zum Zeitpunkt des Ausbruchs der Influenza im Winter die a. F. über dem typischen täglichen absoluten Feuchte-Niveau am jeweiligen Standort liegt oder darunter.
) den täglichen Durchschnittswert von 1972–2002 repräsentiert. In niedrigen Breiten wie den USA ist das absolute Feuchte-Niveau im Winter ohnehin schon wesentlich niedriger als im Sommer (Abbildung 1D). Unter Zuhilfenahme von a. F.′ können wir ermitteln, ob zum Zeitpunkt des Ausbruchs der Influenza im Winter die a. F. über dem typischen täglichen absoluten Feuchte-Niveau am jeweiligen Standort liegt oder darunter.Typischerweise werden ab 4 Wochen vor Ausbruch von Influenza-Epidemien negative a. F.′-Werte beobachtet (Abbildung 2), mit der stärksten Abweichung 17 Tage vor Ausbruch. Dieses Ergebnis bleibt unabhängig vom gewählten Sterblichkeits-Schwellenwert zur Definition des Ausbruchsdatums (übermäßige P&I-Sterblichkeit von 0,001–0,02/100.000 Personen/Tag) stabil. Um die statistische Signifikanz des Zusammenhangs zwischen negativem a. F.′-Wert im Winter und dem Ausbruch von Epidemien zu beurteilen, behandelten wir die Verteilung der a. F.′-Aufzeichnungen zur Winterzeit nach der Bootstrap-Methode und ermittelten eine starke statistische Untermauerung (p < 0,0005, siehe Text S1). Je nach Schwellenwert für die Definition des Ausbruchs ergeben sich im Durchschnitt über die 4 Wochen vor Ausbruch für 55–60% der Ausbruchsdaten negative a. F.′-Werte. Obwohl das Ergebnis statistisch hoch signifikant ist, fällt die beobachtete Verschiebung gegenüber der erwarteten Wahrscheinlichkeit von 50% gering aus. Diese Erkenntnisse indizieren, dass negative a. F.′-Werte für den Ausbruch der Influenza zur Winterzeit nicht erforderlich sind, jedoch eine gesteigerte Wahrscheinlichkeit von Ausbrüchen vorhersagen. Faktisch sorgen negative a. F.′-Werte in den Wochen vor dem Ausbruch für eine zusätzliche Steigerung der Überlebensfähigkeit und Übertragung des Influenzavirus gegenüber den typischen lokalen Niveaus im Winter und können so die Verbreitung des Virus weiter fördern.
Typischerweise werden ab 4 Wochen vor Ausbruch von Influenza-Epidemien negative a. F.′-Werte beobachtet (Abbildung 2), mit der stärksten Abweichung 17 Tage vor Ausbruch. Dieses Ergebnis bleibt unabhängig vom gewählten Sterblichkeits-Schwellenwert zur Definition des Ausbruchsdatums (übermäßige P&I-Sterblichkeit von 0,001–0,02/100.000 Personen/Tag) stabil. Um die statistische Signifikanz des Zusammenhangs zwischen negativem a. F.′-Wert im Winter und dem Ausbruch von Epidemien zu beurteilen, behandelten wir die Verteilung der a. F.′-Aufzeichnungen zur Winterzeit nach der Bootstrap-Methode und ermittelten eine starke statistische Untermauerung (p < 0,0005, siehe Text S1). Je nach Schwellenwert für die Definition des Ausbruchs ergeben sich im Durchschnitt über die 4 Wochen vor Ausbruch für 55–60% der Ausbruchsdaten negative a. F.′-Werte. Obwohl das Ergebnis statistisch hoch signifikant ist, fällt die beobachtete Verschiebung gegenüber der erwarteten Wahrscheinlichkeit von 50% gering aus. Diese Erkenntnisse indizieren, dass negative a. F.′-Werte für den Ausbruch der Influenza zur Winterzeit nicht erforderlich sind, jedoch eine gesteigerte Wahrscheinlichkeit von Ausbrüchen vorhersagen. Faktisch sorgen negative a. F.′-Werte in den Wochen vor dem Ausbruch für eine zusätzliche Steigerung der Überlebensfähigkeit und Übertragung des Influenzavirus gegenüber den typischen lokalen Niveaus im Winter und können so die Verbreitung des Virus weiter fördern.
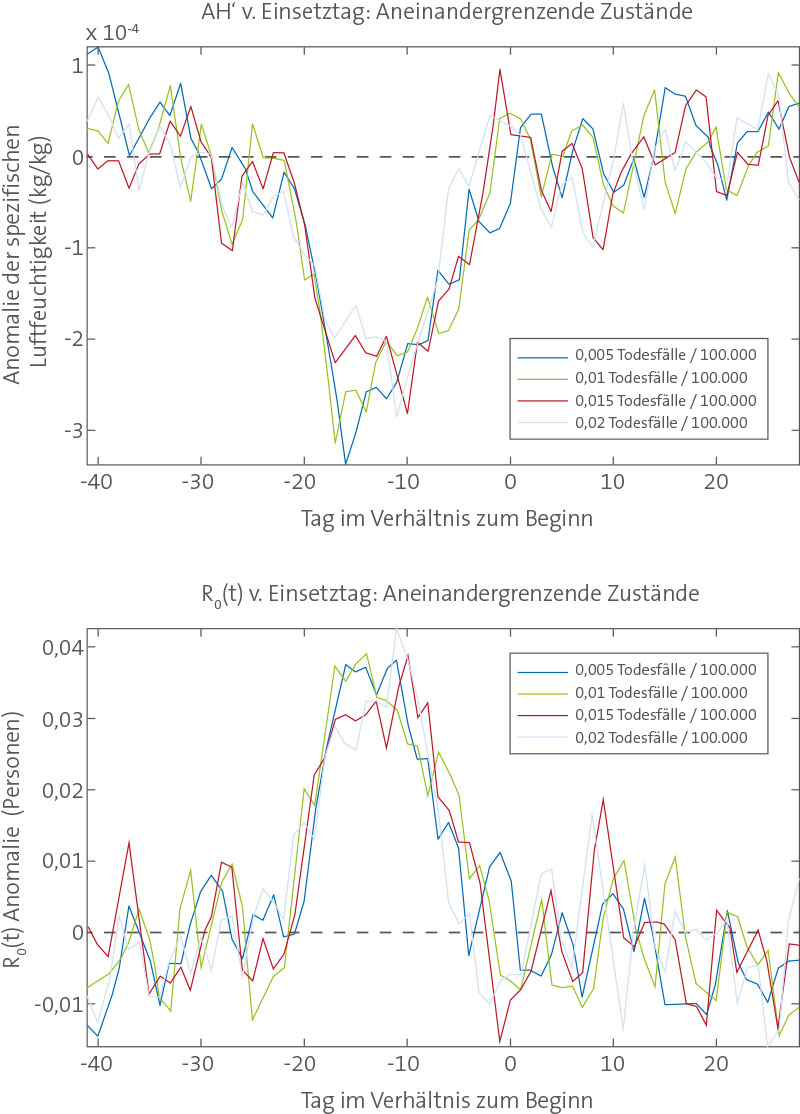
A. F.′ in Verbindung mit dem beobachteten Ausbruchszeitpunkt epidemischer Influenza. Oben, Auftragungen von a. F.′, gemittelt für die Standort-Winter mit einem Influenza-Ausbruch, von 6 Wochen vor bis 4 Wochen nach Beginn des Ausbruchs. Die Bedingungen für jeden der Standort-Winter sind auf Grundlage des Ausbruchsdatums für den jeweiligen Standort-Winter definiert. Das Ausbruchsdatum ist definiert als das Datum, an dem die zur Winterzeit beobachtete übermäßige P&I-Mortalität für zwei aufeinanderfolgende Wochen einen festgelegten Schwellenwert erreicht oder überschritten hat (z. B. 0,01 Todesfälle/100.000 Personen/Tag). Nicht an jedem Standort-Winter kam es zu einem Ausbruch gemäß der Definition über einen festgelegten Ausbruchs-Schwellenwert. Je nach verwendetem Schwellenwert wurden 1181–1420 von 1470 möglichen Epidemien identifiziert (30 Winter für jeden der 48 zusammenhängenden Staaten plus den District of Columbia). Jede durchgehende Linie ist die mit dem Ausbruch der Influenza, definiert durch die Sterblichkeitsrate mit jeweils anderem Schwellenwert, verbundene gemittelte a. F.′ Die gestrichelte Linie zeigt a. F.′ = 0. Unten, Auftragung der R0(t)-Anomalien unter Verwendung der obigen a. F.′-Werte. Die R0(t)-Anomalien werden anhand der besten Combined-Fit-Schätzungen für R0max und R0min berechnet (Tabelle 1). Die gestrichelte Linie zeigt R0(t)′ = 0. doi:10.1371/journal.pbio.1000316.g002 Es zeigen sich außerdem regionale Unterschiede für den Zusammenhang zwischen negativen a. F.′-Werten und dem Ausbruchsdatum. Am ausgeprägtesten ist dieser Zusammenhang im Osten der USA, insbesondere in der Golfregion und dem Nordosten (Abbildungen S2, S3 und S4). Obgleich der Zusammenhang im Westen der USA größtenteils keine statistische Signifikanz erreicht, sind auch in dieser Region die a. F.′-Werte in den Wochen vor dem Ausbruch typischerweise negativ.
Als Nächstes gingen wir nach dem gleichen Ansatz vor, um zu ermitteln, ob andere potenzielle Umwelteinflüsse mit dem Ausbruch der Influenza zur Winterzeit in Verbindung stehen. Aus den Ergebnissen geht hervor, dass negative Abweichungen der relativen Luftfeuchtigkeit und der Temperatur ebenso wie positive Abweichungen der Sonneneinstrahlung ebenfalls das Ausbruchsdatum beeinflussen (Tabelle 1). Die Richtung der Zusammenhänge der täglichen Anomalien von Sonneneinstrahlung und relativer Feuchte zur Winterzeit mit dem Ausbruch von Epidemien ist jedoch dem Zusammenhang zwischen diesen Umweltfaktoren und der epidemischen Aktivität aus saisonaler Sicht entgegengesetzt. Es wurde postuliert, dass eine verminderte Sonneneinstrahlung in den Wintermonaten die Influenza-Aktivität erhöhe, indem sie Melatonin- und Vitamin-D-Level im Wirt und damit seine Resistenz senke [12,13]; unsere Ergebnisse deuten jedoch darauf hin, dass der Ausbruch von Influenza mit einer Anomalie in Form gesteigerter täglicher Sonneneinstrahlung assoziiert ist. Ähnlich verhält es sich mit der relativen Feuchte, die im Winter am höchsten ist [11], während der Ausbruch von Influenza mit Anomalien in Form niedriger relativer Feuchte in Zusammenhang gebracht wird.
Möglicherweise können die beobachteten Korrelationen zwischen diesen meteorologischen Anomalien und dem Ausbruch von Influenza durch spezifische Wettermuster erklärt werden. Außergewöhnlich niedrige absolute Feuchtewerte in den kontinentalen USA hängen üblicherweise mit dem Einstrom kälterer Luftmassen aus dem Norden zusammen. Diese Luftmassen, die häufig einer Kaltfront folgen, bringen wolkenlose Himmel (d. h. erhöhte Sonneneinstrahlung) sowie sinkende Oberflächentemperaturen und Luftfeuchtigkeitsniveaus mit sich. Während die Luftmasse sich nach Süden bewegt, wärmt sie sich langsam auf; sofern sie jedoch keine ausgedehnten offenen Gewässer überquert, nimmt die absolute Feuchte dabei kaum zu. In der Folge können sich in diesen Luftmassen auch ungewöhnlich niedrige relative Feuchte-Niveaus entwickeln. Über ihren Zusammenhang mit Wetterbedingungen, die negative a. F.′-Werte in eine Region bringen, könnten die Anomalien von Sonneneinstrahlung und r. F. demnach akausal mit dem Ausbruch von Influenza verknüpft sein.
Temperatur und absolute Luftfeuchtigkeit sind stark miteinander korreliert (Tabelle S1); beide sind im Winter am niedrigsten, wenn die Übertragungsrate von Influenza einen Höchststand erreicht, und für beide besteht ein Zusammenhang zwischen negativen Anomalien und dem Ausbruch von Influenza. Diese Tendenzen stimmen mit den aus Labordaten gefolgerten Zusammenhängen überein [11,14,15]. Für die Bestimmung, welche dieser Variablen für das Ausbrechen am bedeutendsten ist, stützen wir uns auf vorhandene Laboranalysen, die den Einfluss beider Umweltfaktoren untersucht und ergeben haben, dass die absolute Feuchtigkeit der wesentliche Faktor für das Überleben und die Übertragung des Influenzavirus ist [11]. Des Weiteren ist a. F.′ die einzige Anomalievariable, deren Zusammenhang mit dem Ausbruch für alle vier Schwellenwerte signifikant ist (mit p < 0,00002) (Tabelle 1).

Zusammenhang täglicher Anomalien verschiedener Umweltvariablen mit dem Ausbrechen von Influenza zur Winterzeit von 1972–2002 für die zusammenhängenden USA
Zudem ist zu beachten, dass die saisonalen Temperaturbedingungen in Innenbereichen, in denen die meisten US-Bewohner den Großteil ihrer Zeit verbringen, oft stark reguliert sind. Im Freien können sich die Tagesdurchschnittstemperaturen zwischen Sommer und Winter um mehr als 20°C unterscheiden, während dieser Temperaturkreislauf in Innenbereichen durch Heizung und Klimaanlagen stark reduziert wird. Für die absolute Feuchte dagegen besteht sowohl in Innenbereichen als auch im Freien ein ausgeprägter saisonaler Kreislauf [11].
Modellsimulationen der Saisonalität von Influenza
Zur weiteren Untersuchung der Hypothese, dass die absolute Feuchte als fundamentale Triebkraft der Saisonalität von Influenza fungiert, analysierten wir, ob ein Modell der mittels Bedingungen absoluter Feuchte erzwungenen Influenza-Übertragung auf Bevölkerungsebene die beobachteten saisonalen Muster der P&I-Sterblichkeit reproduzieren kann. Dazu simulierten wir die Übertragung von Influenza in fünf Staaten, repräsentativ für verschiedene Klimaregionen innerhalb der USA: Arizona, Florida, Illinois, New York und Washington.
Das Modell berücksichtigt drei Krankheitsklassen: suszeptibel, infiziert und genesen. Um den Einfluss abnehmender Immunität infolge von Antigendrift zu integrieren, erlauben wir Individuen mit einer definierten Rate, in die suszeptible Klasse zurückzukehren (SIRS-Modell für susceptible, infected, recovered, susceptible). Zwischen 1972 und 2002 beobachtete tägliche AH-Bedingungen in jedem Staat werden verwendet, um die Basisreproduktionszahl R0(t) des Influenzavirus zu modulieren, d. h. die Übertragungsrate pro Generation in einer vollständig suszeptiblen Bevölkerung. Diese täglichen Fluktuationen von R0(t) modifizieren innerhalb des SIRS-Modells die Übertragungswahrscheinlichkeit pro Kontakt und beeinflussen so die Übertragungsdynamik von Influenza. Das SIRS-Modell umfasst vier freie Parameter: zwei (R0max und R0min), die den Wertebereich von R0(t) definieren, einen für die Dauer der Immunität (D) und einen für die Dauer der Infektiosität (L).
Wenn die absolute Luftfeuchtigkeit die Saisonalität der Influenza steuert, sollten die Simulationen des von der absoluten Feuchte abhängigen Übertragungsmodells mit der besten Anpassung (Best-Fit-Simulationen) folgende Kriterien erfüllen: 1) der mittlere jährliche Modellkreislauf der Infektion sollte mit Beobachtungen in jedem Staat übereinstimmen; 2) diese Simulation sollte gegen vergleichbare Parameterwerte konvergieren, d. h. die Virusreaktion auf die a. F. sollte in den verschiedenen Staaten konstant sein; und 3) die Modulation der Übertragungsraten (R0(t)) durch die a. F. innerhalb des Modells muss mit dem aus Labordaten hervorgehenden großen Wertebereich übereinstimmen (Abbildung 1).
In jedem der fünf Staaten wurden mehrere 31-Jahr-Simulationen (1972–2002) mit zufällig gewählten Parameterkombinationen durchgeführt. Wir haben dann den mittleren Jahresverlauf täglicher Infektionen aus jeder Simulation mit einem entsprechenden Durchschnitt der zwischen 1972 und 2002 beobachteten übermäßigen P&I-Sterblichkeitsraten verglichen [3,4]. Die Best-Fit-Modellsimulationen an jedem Standort spiegeln den beobachteten jährlichen Kreislauf von Influenza wider (Abbildung 3). Diese Simulationen erzeugen nicht nur den Anstieg von Übertragung und Infektion zum Jahresende, sondern auch den Peak zur Winterzeit Anfang Januar sowie typischerweise einen schwächeren Peak Ende Februar/Anfang März. Für Modelle und Beobachtungen gleichermaßen gilt, dass diese doppelten Peaks zur Winterzeit typischerweise nicht in einzelnen Jahren auftreten. Vielmehr stellen diese Epidemie-Verläufe die Mittelung der einzelnen Ausbrüche dar, die üblicherweise ihren Höhepunkt zwischen Dezember und April erreichen (Abbildung S5).
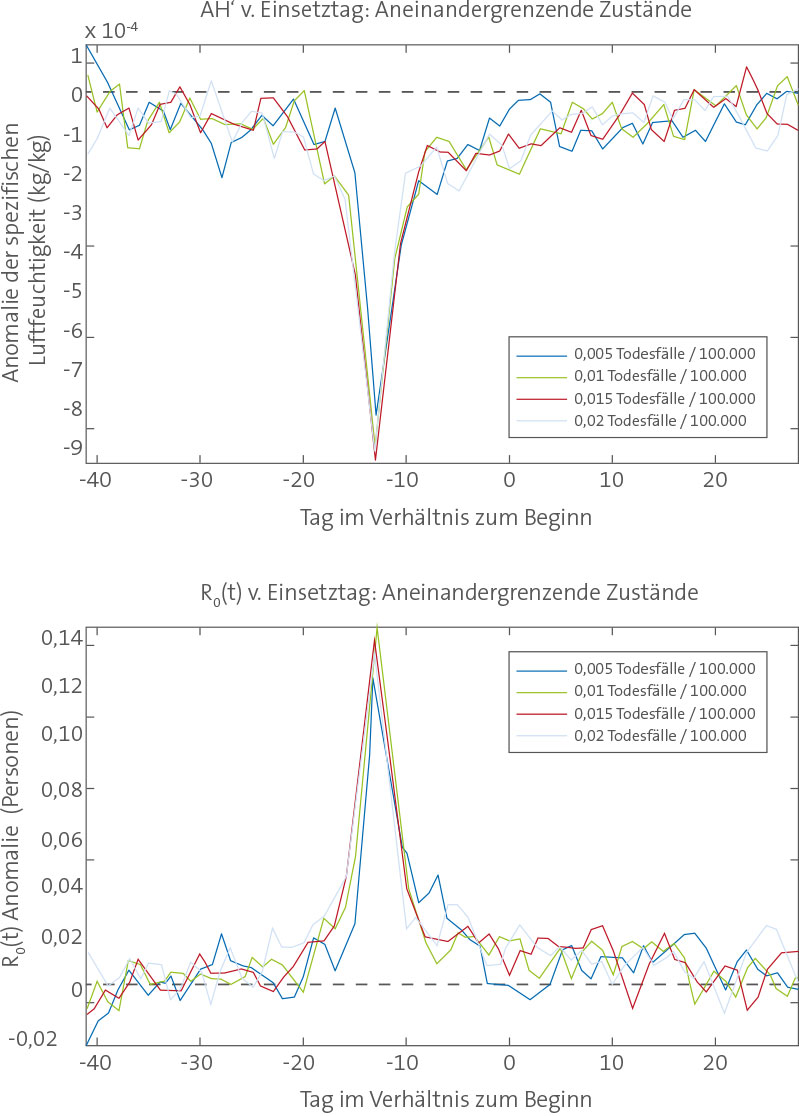
Mittlere Jahreskreisläufe der Best-Fit-SIRS-Modellsimulationen in den fünf Staaten. Hier wurden die Best-Fit-Simulationen für jeden Staat einzeln basierend auf dem RMS-Fehler nach Skalierung des 31-jährigen Mittels täglicher Infektionszahlen auf das 31-jährige Mittel beobachteter täglicher übermäßiger P&I-Sterblichkeitsraten ausgewählt. Die dicke blaue Linie zeigt die Best-Fit-Simulation; die dünneren grünen Linien zeigen die neun nächstbesten Simulationen. doi:10.1371/journal.pbio.1000316.g003
Wir haben außerdem die am besten passenden Parameterkombinationen für eine gemeinsame Bewertung aller fünf Standorte gesucht. Diese Parameterkombinationen der besten „kombinierten Anpassungen“ (Combined Fits) zeichnen sich aus durch eine hohe R0max (typischerweise > 2,8), hohe R0min (> 1) und einen kurzen mittleren infektiösen Zeitraum (2 < D < 4,2 Tage) (Abbildung S6; Tabelle 2). Die Best-Fit-Simulationen an den fünf separaten Standorten nehmen einen vergleichbaren Parameterraum ein (Abbildungen S7, S8, S9, S10 und S11; Tabelle S2). Insbesondere konvergieren diese Simulationen gegen eine hohe R0max, was eine vergleichbare Reaktion auf Variationen der absoluten Feuchte andeutet (siehe Text S1).
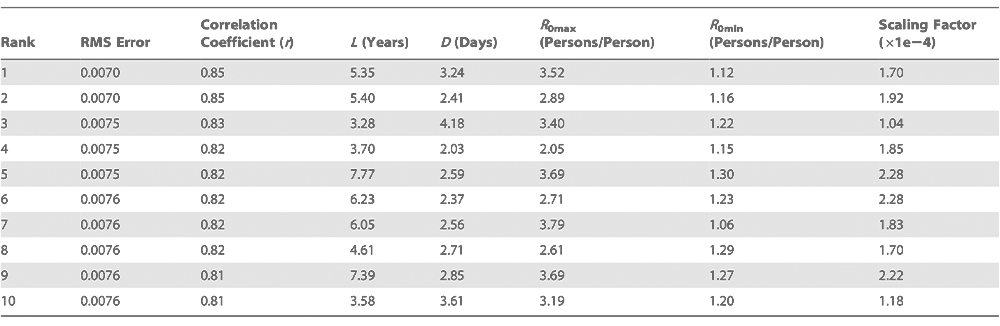
Parameterkombinationen für die zehn Best-Fit-Simulationen an den Standorten Arizona, Florida, Illinois, New York State und Washington State
In Simulationen, die gut mit den beobachteten übermäßigen P&I-Sterblichkeiten übereinstimmen, besteht eine Korrelation unter den Parameterwerten des SIRS-Modells. Beispielsweise sind L und D in gut passenden Simulationen meist umgekehrt proportional (Abbildungen S6, S7, S8, S9, S10 und S11). Zudem können offenbar weite Bereiche des Parameterraums hochwertige Simulationen mit niedrigem Root-Mean-Square-(RMS-)Fehler generieren (Abbildung S6). Möglicherweise tragen die stochastischen Komponenten des SIRS-Modells einen Teil zu diesem Verhalten bei. Die flach verlaufende Anpassungsgüte (Goodness of Fit) innerhalb des Modell-Parameterraums deutet darauf hin, dass es nicht eine „beste“ Parameterkombination gibt, sondern dass Parameterkombinationen in ganzen Wertebereichen gute Simulationen der Übertragung von Influenza erzeugen können. Diese Wertebereiche sind: L = 3–8 Jahre, D = 2–3,75 Tage, R0max = 2,6–4 und R0min = 1,05–1,30. Wir führten wiederholte SIRS-Modellierungen unter Anwendung dieser Teilbereiche des Parameterraums durch. Best-Fit-Simulationen aus diesem Teilbereich des Parameterraums (Tabelle S3) waren von vergleichbarer Qualität und zeigten die gleiche flach verlaufende Anpassungsgüte innerhalb des Modell-Parameterraums wie die in Tabelle 2 dargestellten Best-Fit-Simulationen.
Da das SIRS-Modell nur mit Influenza verbundene Infektionen simuliert, nicht aber Todesfälle, ist ein Skalierungsfaktor erforderlich, um die im Modell simulierten Infektionsraten mit den beobachteten übermäßigen P&I-Sterblichkeitsraten vergleichen zu können. Dieser Skalierungsfaktor kann als die Todesfallrate verstanden werden, also die Sterbewahrscheinlichkeit nach Infektion. Es beruhigt, dass alle Best-Fit-Simulationen einen Skalierungsfaktor in der gleichen Größenordnung erzeugen, der zudem grob mit dem erwarteten Wert der Todesfallrate für P&I-induzierte Todesfälle übereinstimmt (siehe Text S1). Das Modell erklärt auch regionale Variationen der Influenza-Dynamik. Aufgrund der modellierten nichtlinearen Beziehung zwischen R0(t) und a. F. (Abbildung 1C) ist der saisonale Kreislauf von R0(t) sowohl abhängig von der Amplitude des saisonalen Verlaufs der absoluten Feuchte als auch von den mittleren absoluten Feuchtewerten (Abbildung 1D und 1E). In Florida sind die mittleren absoluten Feuchtewerte höher als in den anderen vier Staaten, aber der saisonale a. F.-Verlauf bleibt dynamisch und erzeugt einen saisonalen R0(t)-Kreislauf mit ausreichender Amplitude für das Auslösen einer effektiven Reproduktionszahl, RE(t)= R0(t) *S(t)/N, größer 1 (Abbildung 1F) und das Hervorrufen von Influenza-Epidemien vornehmlich im Winter.
Dieser Phasenverlauf wird durch die Ausbruchsdynamik noch verstärkt, da Epidemien zur Winterzeit in einem Großteil der Modellbevölkerung Immunität hervorrufen, welche dann die Suszeptibilität auf Bevölkerungsebene im Verlauf des nächsten Sommers senkt, wenn R0(t) niedrig ist. In Arizona und Washington State ist der saisonale a. F.-Kreislauf weniger stark ausgeprägt als in den anderen drei Staaten, aber die durchschnittlichen absoluten Feuchte-Niveaus sind niedriger und in einem Bereich, für den die Laborergebnisse eine höhere Sensitivität für Variationen der a. F. erkennen lassen; in der Folge bleibt für R0(t) ein nennenswerter saisonaler Kreislauf erhalten (Abbildung 1E). Für alle fünf Staaten ist die durch absolute Feuchte bedingte saisonale Variation von R0(t) so ausgeprägt, dass RE(t) stark durch Bedingungen absoluter Feuchte moduliert wird und im Winter, wenn es zu Ausbrüchen kommt, 1 übersteigt (Abbildung 1F).
Die auf Luftfeuchtigkeit basierenden SIRS-Simulationen erfüllen unsere drei aufgestellten Kriterien und unterstützen damit die Hypothese, dass die Saisonalität von Influenza in gemäßigten Zonen durch die absolute Feuchtigkeit kontrolliert wird. Die Simulationen produzieren in den fünf klimatologisch verschiedenen US-Staaten unter Verwendung vergleichbarer Parameterwerte übereinstimmende Ergebnisse. Die hohe Abhängigkeit der simulierten Influenza-Übertragung von der absoluten Feuchte stimmt mit der Analyse von Laborexperimenten überein, die große Veränderungen in der Überlebensfähigkeit und der Übertragung des Influenzavirus in Reaktion auf Variation der absoluten Feuchte gezeigt haben (Abbildung 1A und 1B).
Kreuzvalidierung der Modellergebnisse
Zur weiteren Validierung der Erkenntnisse aus dem SIRS-Modell haben wir ermittelt, ob die aus den fünf ausgewählten Staaten hervorgegangenen Best-Fit-Simulationen die saisonalen Verläufe der Influenza an anderen Standorten in den USA reproduzieren können. Unter Verwendung der zehn besten Combined-Fit-Parameterkombinationen (Tabelle 2) wurden SIRS-Simulationen über 31 Jahre (1972–2002) in jedem der 48 zusammenhängenden US-Staaten und DC durchgeführt.
Die Ergebnisse dieser Kreuzvalidierung zeigen für die Mehrzahl der Staaten gute Simulationen der beobachteten übermäßigen P&I-Sterblichkeit (im Durchschnitt r > 0,7, mindestens r > 0,5, siehe Methoden und Tabelle 3).
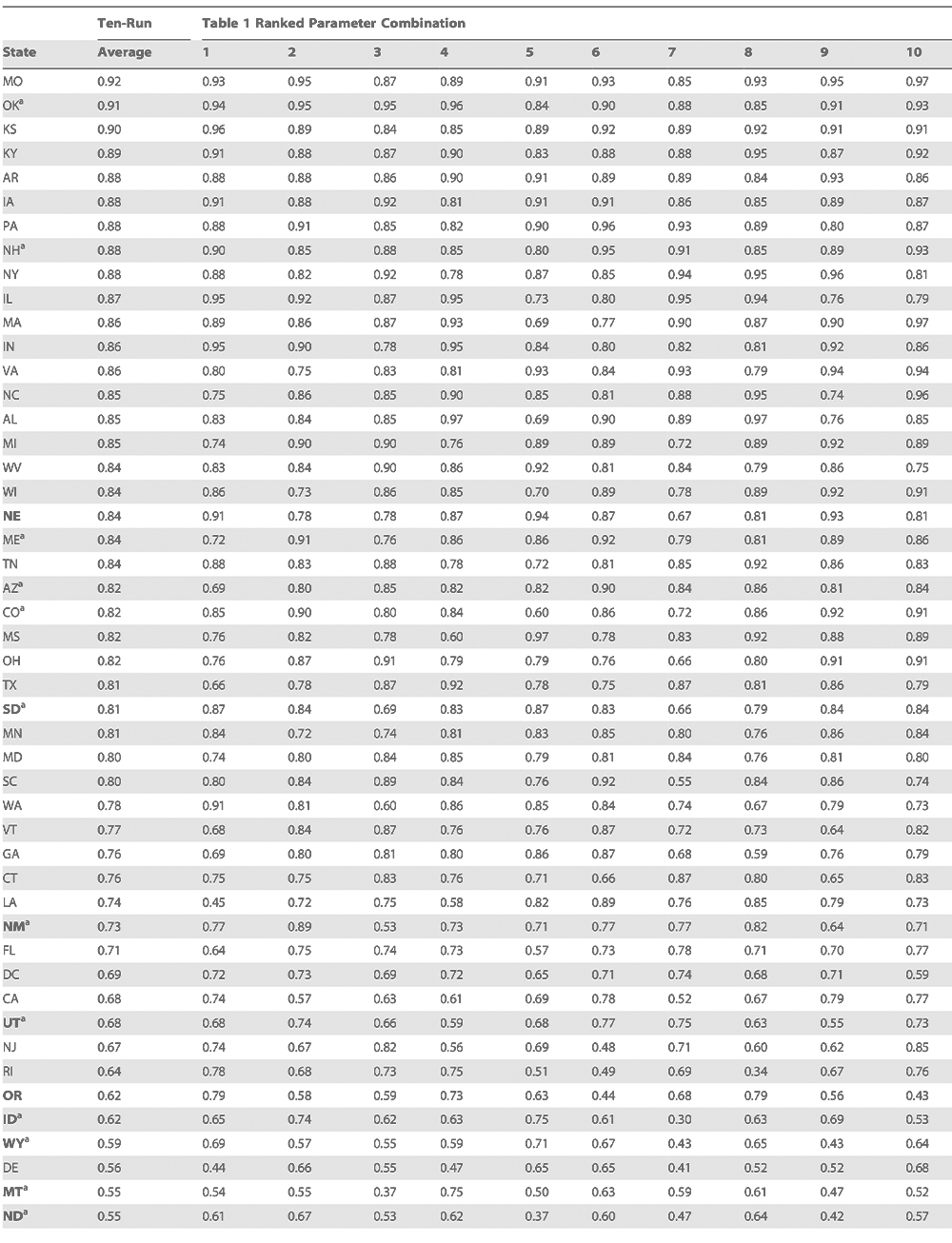
Korrelationskoeffizienten für das SIRS-simulierte Auftreten von Influenza zwischen 1972 und 2002 in den zusammenhängenden USA und dem District of Columbia mit der zwischen 1972 und 2002 beobachteten übermäßigen P&I-Sterblichkeit
Einige Staaten, insbesondere die dünn besiedelten westlichen Staaten, erbringen weniger gute Ergebnisse. Diese Staaten haben oft einen schwach ausgeprägten Workflow [4], wodurch die Einführungsrate des Virus jeden Winter verringert sein könnte. Zudem sorgen heterogene absolute Feuchte-Bereiche innerhalb einzelner (insbesondere großer) Staaten für Fehler, da die Simulation mit einem einzigen Durchschnitts-a. F.-Wert für den gesamten Staat arbeitet. Dreizehn Staaten der kontinentalen USA, einschließlich Arizona, weisen geringe Workflow-Raten auf [4]. Sechs dieser 13 Staaten sind unter den zehn in der Kreuzvalidierung am schlechtesten abschneidenden; es ist unwahrscheinlich, dass ein solches Clustering nur zufällig auftritt (p < 0,005). Weiterhin sind sieben der am schlechtesten abschneidenden Staaten unter den zehn am wenigsten dicht besiedelten (p < 0,0001).
Insgesamt zeigt die Kreuzvalidierung, dass die besten Combined-Fit-Parameterkombinationen die Saisonalität von Influenza im gesamten Land simulieren können. In Zukunft könnte die Verwendung höher aufgelöster absoluter Feuchte- und beobachteter P&I-Daten, die die lokalen Bedingungen genauer repräsentieren, diese Modellergebnisse noch verbessern.
Zusätzliche SIRS-Modellergebnisse
Wir haben die SIRS-Modellsimulationen auch eingesetzt, um den Zusammenhang zwischen negativer a. F.′ und dem Ausbruch von Epidemien weiter zu untermauern (Abbildung 2). Best-Fit-Durchläufe des SIRS-Modells offenbaren, dass etwa 2 Wochen vor Ausbruch (definiert über die SIRS-Modell-Infektionsraten; Abbildung 4) ein stark negativer a. F.′-Wert zu beobachten ist. Die Verzögerungszeit unterscheidet sich um eine Woche zwischen dieser Analyse mit Modell-Infektionsraten (2 Wochen) und der Analyse mit beobachteten übermäßigen P&I-Sterblichkeitsraten (3 Wochen); dieser Unterschied entspricht grob der medianen Zeit zwischen Infektion und Tod [16–18]. Der breitere Peak negativer a. F.′ in Abbildung 2 ist vermutlich durch andere Faktoren zu erklären, die in der realen Welt die Art des Ausbruchs beeinflussen und im SIRS-Modell nicht berücksichtigt sind (siehe Text S1). Schließlich haben wir untersucht, ob der Schulkalender, der die Raten direkten Personenkontakts modifiziert, eine bessere Simulation der saisonalen Influenza liefern kann als die absolute Feuchte. Schätzungen zufolge führen Schulferien zur Veränderung der Übertragungsrate von Influenza um ca. 25% [19]. In den USA finden diese Ferien über den Sommer, am Ende des Kalenderjahres sowie im Frühling statt.
Es wurde eine Reihe von SIRS-Modellsimulationen durchgeführt, in der über das Schuljahr hinweg eine schrittweise Vergrößerung von R0(t) enthalten war (siehe Text S1). Simulationen, in denen allein das Schließen der Schulen R0(t) moduliert wurde, konnten zwar einen saisonalen Kreislauf der Influenza mit Schwerpunkt auf dem Winter erzeugen, jedoch konnten diese Simulationen die beobachtete übermäßige P&I-Sterblichkeit nicht so gut reproduzieren wie solche mit der absoluten Feuchtigkeit als einzigem Faktor (siehe Abbildungen S14 und S15; Tabelle S5; Text S1). Zudem war eine Änderung der Influenza-Übertragung (R0(t)) um 40–90% erforderlich, um diese Saisonalität auszulösen (Tabelle S5). Dieses Spektrum für Änderungen von R0(t) ist etwas breiter als die zuvor geschätzte Modulation von ca. 25 %; diese vorherigen Schätzungen waren allerdings aus einem nach Alter gegliederten Bevölkerungsmodell abgeleitet, was einen direkten Vergleich erschwert.
Diskussion
Es ist schwierig, eine Unterscheidung zwischen allen potenziellen Umwelteinflüssen auf die Saisonalität der Influenza – wie absolute Luftfeuchtigkeit, relative Luftfeuchtigkeit, Temperatur, Sonneneinstrahlung und dem Schulkalender – zu treffen, da sie alle eine ähnlich ausgeprägte jährliche Periodizität aufweisen. Trotzdem deuten unsere Ergebnisse darauf hin, dass die absolute Feuchte ein wesentlicher (und wahrscheinlich der vorrangige) Einflussfaktor für die Saisonalität der Influenza ist. Gründe dafür sind: 1) der empirische Zusammenhang zwischen negativer a. F.′ und dem Auftreten von Influenza-Ausbrüchen zur Winterzeit (Abbildung 2), der statistisch stärker ist als für die relative Feuchtigkeit, die Temperatur oder die Sonneneinstrahlung (Tabelle 1); 2) die relative Beständigkeit der Reaktion auf die absolute Feuchte in den fünf Staaten, die im Detail modelliert wurden (d. h. vergleichbarer Parameterraum; Tabelle S2); und 3) das Ergebnis der SIRS-Kreuzvalidierung, dass die gleichen Best-Fit-Parameter (Tabelle 2) in einem Großteil der USA erfolgreiche Simulationen der Influenza-Saisonalität hervorbringen können (Tabelle 3).
Zusätzlich widersprechen mehrere Erkenntnisse der Hypothese, dass der Zusammenhang der absoluten Feuchte mit dem saisonalen Kreislauf der Influenza nur auf der Vermischung mit anderen potenziellen Triebkräften beruhe. Ihr unplausibler positiver Zusammenhang mit dem Ausbrechen der Influenza zur Winterzeit schwächt die Argumente für einen Einfluss der Sonneneinstrahlung. Obwohl Laboranalysen ergeben haben, dass eine niedrige relative Luftfeuchte das Überleben und die Übertragung von Influenza fördert, verläuft die relative Feuchte in der Außenumgebung in Phasen, die dieser Hypothese widersprechen (maximal im Winter, minimal im Sommer), und kann keine Erklärung für den Höhepunkt des Auftretens von Influenza im Winter liefern.
Die Argumente für die Temperatur als Einflussfaktor werden durch die kleine Amplitude ihres jährlichen Verlaufs in den meisten Innenbereichen geschwächt. Schließlich deuten Reanalysen von Laborexperimenten darauf hin, dass die absolute Feuchte die beste Einzelvariable zur Modulierung des Überlebens und der Übertragung des Influenzavirus darstellt [11]; Zusammenhänge mit Temperatur und relativer Feuchte spiegeln wahrscheinlich lediglich ihre positive Kovariabilität mit der absoluten Feuchte in verschiedenen Zeiträumen wider. Trotzdem kann die Möglichkeit einer Bedeutung von Temperatur oder anderen (möglicherweise mehreren) Kovariablen nicht völlig unberücksichtigt gelassen werden. Weitere Laboruntersuchungen sind erforderlich, um die Auswirkungen von Luftfeuchtigkeit, Verdunstung und Temperatur auf die Proteinstruktur und das Überleben des Virus beurteilen zu können.
Aus den SIRS-Modellsimulationen geht auch hervor, dass der Schulkalender, obwohl er das saisonale Auftreten von Influenza-Epidemien erklären kann, nicht so gut mit Beobachtungsdaten korrespondiert wie Simulationen mit absoluter Feuchte als treibender Kraft (Abbildungen S14 und S15). Der erforderliche Anstieg der Übertragbarkeit außerhalb der Ferien ist größer als bisher angenommen; mit einer so großen Variation in der Übertragung kommt es zu einer auffälligen Abnahme der Übertragung in den Weihnachts- und Frühlingsferien, die aus Beobachtungsdaten so nicht erkennbar ist (siehe Text S1). Trotzdem ist ein Effekt geschlossener Schulen auf die Übertragungsraten von Influenza bereits gut dokumentiert [19,20] und sollte nicht außer Acht gelassen werden. Es ist sicher möglich, dass die Auswirkungen der absoluten Feuchte und des Schulkalenders auf die Influenza-Übertragung zusammenwirken; unsere Erkenntnisse aus statistischen Analysen und dem SIRS-Modell deuten jedoch darauf hin, dass die absolute Feuchte-Variabilität eine genügsamere Erklärung für die Saisonalität der epidemischen Influenza in gemäßigten Zonen bereitstellt und zudem mit dem Ausbruchsdatum der einzelnen Influenza-Epidemien zur Winterzeit in Verbindung steht.
Die These, dass die absolute Feuchte zumindest teilweise die Saisonalität der Influenza bestimmt, wird gestützt durch: 1) Labornachweise [11]; 2) die wesentlich schwächer ausgeprägte Saisonalität in den Tropen, wo die Luftfeuchtigkeit das ganze Jahr über hoch ist, aber ein Schulkalender existiert; 3) die a. F.′-Ausbruchsanalyse (Abbildungen 2 und 4); 4) die Plausibilität der Parameterkombinationen und der Effektstärke der a. F. in SIRS-Modellsimulationen (Abbildungen 1 und 3; Tabelle 2); und 5) die insgesamt überragende Qualität a. F.-forcierter Simulationen (Abbildung S14) und ihre verringerte Anfälligkeit für stochastische Prozesse innerhalb des SIRS-Modells (Abbildung S15).
Zwischen den verschiedenen Standorten bestehen geringfügige Unterschiede der Best-Fit-Parameterwerte für das SIRS-Modell (Abbildungen S7, S8, S9, S10 und S11; Tabelle S2), von denen einige vom Wirt ausgehen könnten. Florida und New York beispielsweise zeigen eine Tendenz zu einer kürzeren Dauer der Immunität. Dieser Unterschied könnte auf einer Reihe vom Wirt ausgehender Faktoren beruhen, die für diese Staaten spezifisch sind. Die hier präsentierten Ergebnisse schließen einen Einfluss solcher Faktoren auf die Übertragung und Saisonalität von Influenza nicht aus. Unterschiede in der Suszeptibilität und Infektiosität der Bevölkerung (z. B. Alter und allgemeine Gesundheit der Bevölkerung), saisonale Variationen des Wirtsverhaltens (z. B. mehr Zeit in Innenräumen und enger Kontakt im Winter [19]) und Wirtsresistenz (z. B. Melatonin- oder Vitamin-D-Mangel im Winter [12,13]) können nach wie vor die Übertragungsraten von Influenza beeinflussen.
Zwischen den Staaten gibt es auch Unterschiede in den durchschnittlichen Peaks der SIRS-simulierten RE(t) (Abbildung 1F); allerdings besteht an den Standorten keine systematische Beziehung zwischen beobachteten übermäßigen P&I-Sterblichkeitsraten und diesen RE(t)-Spitzenwerten. In Florida und New York sind beispielsweise die beobachteten Sterblichkeitsraten pro 100.000 Personen ähnlich, aber die Spitzenwerte für RE(t) unterscheiden sich. Kontaktraten sowie Alter und Struktur der Bevölkerungen unterscheiden sich von Staat zu Staat. Diese Unterschiede, insbesondere der Anteil an Senioren, welche im Verlauf der saisonalen Epidemien das höchste Risiko tragen, an Influenza zu sterben, haben zweifellos einen Einfluss auf die Infektions- und Sterblichkeitsraten durch Influenza und modulieren die Amplitude und die Dauer der einzelnen Ausbrüche. Zudem ist auch der dominante Influenza-Subtyp in jeder Saison ein wesentlicher Prädiktor für die influenzabedingte Sterblichkeit; A/H3N2-dominierte Saisons bringen zwei- bis dreimal höhere Todesraten mit sich als H1N1- und B-dominierte Saisons [3,4]. Diesen anderen Faktoren wird in unserem SIRS-Modell nicht Rechnung getragen; aus diesem Grund gibt es keine gute Eins-zu-eins-Übereinstimmung zwischen der durchschnittlichen Peakhöhe von RE(t) und den beobachteten übermäßigen P&I-Sterblichkeitsraten. Allerdings besteht auch im SIRS-Modell eine Beziehung zwischen RE(t) und simulierten Infektionsraten. Unter den zehn Best-Fit-Simulationen je Standort entsprechen die durchschnittlichen maximalen E(t)-Werte (von groß nach klein) New York, Illinois, Washington, Arizona und Florida. Ähnlich verhält es sich mit den durchschnittlichen maximalen Epidemiegrößen, die (von groß nach klein) mit New York, Washington, Illinois, Arizona und Florida übereinstimmen. Dieser recht direkte Zusammenhang ist nicht unerwartet; innerhalb des SIRS-Modells korrespondieren höhere RE(t)-Werte unmittelbar mit stärkerer Übertragung und in der Folge mit der schnelleren Entstehung größerer Ausbrüche.
Es ist zu beachten, dass die beobachtete P&I-Sterblichkeit ein imperfekter Indikator für das Auftreten von Influenza ist, da andere Atemwegserkrankungen ähnliche saisonale Periodizitäten aufweisen. Zweifellos tragen auch diese anderen Krankheiten zur Saisonalität der hier verwendeten empirischen Zeitreihe bei (Abbildung 3, Abbildung S1). Dennoch weist die übermäßige P&I-Sterblichkeit generell eine starke Übereinstimmung mit anderen Indikatoren des Auftretens von Influenza wie Daten zu Krankenhauseinweisungen und Labormeldungen auf [4]. Ein klareres Bild des Einflusses von Umweltfaktoren auf die Saisonalität und das Ausbrechen von Influenza wird sich dann ergeben, wenn die Effekte der absoluten Feuchte und anderer Umweltvariablen auch auf andere möglicherweise zeitgleich auftretende saisonale Erreger von Atemwegserkrankungen näher beleuchtet werden.
Die ersten Belege dafür, dass das Überleben und die Übertragung des Influenzavirus durch die absolute Feuchte beeinflusst werden, wurden aus Laborexperimenten gewonnen, die die luftgetragene Übertragung von Influenza untersucht haben; unser SIRS-Modell arbeitet jedoch mit keinem spezifischen Übertragungsweg. Daher könnten auch andere Übertragungswege, insbesondere eine indirekte Übertragung über Infektionsträger, sofern sie in gleichem Maße von der absoluten Feuchte abhängig sind, ebenfalls zur Saisonalität von Influenza in gemäßigten Zonen beitragen. Zudem ist das SIRS-Modell hoch idealisiert, und viele Faktoren der realen Welt, die Einfluss auf die Übertragungsraten haben können, werden nicht repräsentiert. Dazu zählen Ballungsräume, strukturierte Interaktionen, Variationen der Wirts-Infektiosität und mehrere Influenza-Stämme, für die verschiedene Grade der Kreuzimmunität auftreten.
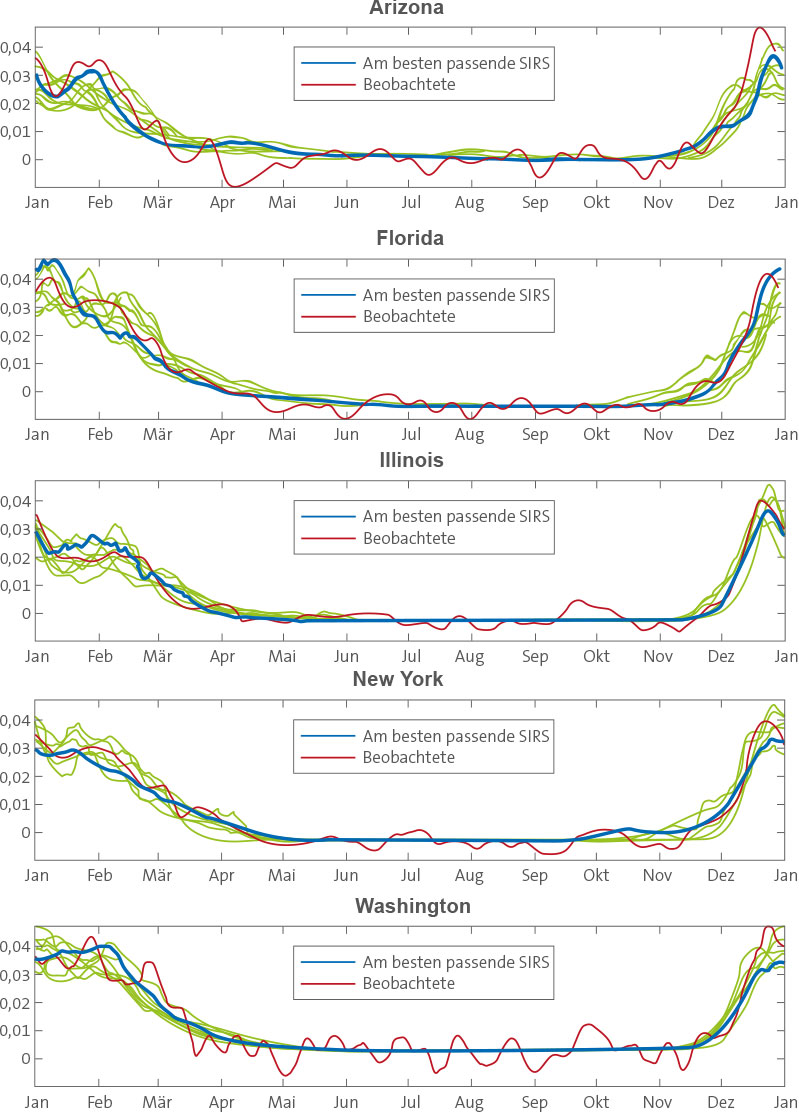
Abbildung 4
Mit dem SIRS-simulierten Influenza-Ausbruch verbundene a. F.′ Oben, Auftragungen der mittleren a. F.′ in Verbindung mit dem Ausbruch von Influenza zur Winterzeit für die zehn Best-Fit-SIRS-Modellsimulationen in den fünf Staaten (Arizona, Florida, Illinois, New York und Washington). Das Ausbruchdatum ist definiert als das Datum, an dem die Infektionsraten zur Winterzeit für zwei aufeinanderfolgende Wochen ein festgelegtes Niveau erreicht oder überschritten haben (z. B. 50 Infektionen/100.000 Personen/Tag). Jede durchgezogene Linie ist die mit dem Ausbruch von Influenza verbundene gemittelte a. F.′, definiert durch eine jeweils andere Schwellen-Infektionsrate. Die gestrichelte Linie zeigt a. F.′ = 0. Unten, Auftragungen der R0(t)-Anomalien unter Verwendung der a. F.′-Werte. Die R0(t)-Anomalien werden unter Verwendung der Parameter R0max und R0min aus jeder Best-Fit-Simulation berechnet (Tabelle S3). Die gestrichelte Linie zeigt R0(t)′ = 0. doi:10.1371/journal.pbio.1000316.g004
Zukünftige Untersuchungen könnten diese Effekte in ein realistischeres Influenza-Modell einbinden, das auch die Effekte der absoluten Feuchtigkeit berücksichtigt. Das würde auch eine bessere Unterscheidung zwischen den Auswirkungen des Schuljahres und der absoluten Feuchte ermöglichen. Auch sollten die Effekte der absoluten Feuchte auf die Übertragung von Influenza in Modelle eingebunden werden, die Reisen und Workflow betrachten [4,21,22], um die saisonale geografische Verbreitung der Influenza zu erklären.
Die hier präsentierten Analysen müssen auf weitere Gebiete ausgeweitet werden, etwa die Tropfen, wo die absolute Feuchte das ganze Jahr über hoch ist und die Saisonalität der Influenza oft weniger klar definiert ist. Eine hohe absolute Feuchte schließt das Überleben und die Übertragung des Influenzavirus nicht aus, sie reduziert diese lediglich. Es ist also möglich, dass die absolute Feuchte auch in den Tropen eine Rolle spielt.
Allerdings deuten die hier dargestellten Ergebnisse darauf hin, dass R0(t) in Gebieten mit ganzjährig hoher absoluter Feuchte wie den Tropen weniger abhängig von der a. F.-Variabilität wäre. Damit wiederum könnten andere, möglicherweise vom Wirt ausgehende Faktoren einen dominanteren Einfluss auf die saisonale Variabilität des Auftretens von Influenza ausüben. Laborstudien haben den ersten Nachweis geliefert, dass die a. F. die Saisonalität der Influenza in gemäßigten Zonen steuern könnte [11]. Das hier dargelegte Modell und die statistischen Ergebnisse deuten darauf hin, dass die im Labor beobachteten Effekte der absoluten Feuchte ausreichend sind, um die auf Bevölkerungsebene auftretenden Muster zu erklären, und sie demonstrieren das Leistungsvermögen epidemiologischer Modellierungen, die auf Experimenten auf individueller Ebene beruhen. Die Ergebnisse deuten darauf hin, dass die absolute Feuchte sowohl die Saisonalität des Auftretens von Influenza als auch den Zeitpunkt einzelner Influenza-Ausbrüche zur Winterzeit in gemäßigten Zonen beeinflusst. Der Zusammenhang negativer a. F.′-Werte mit dem Ausbrechen von Influenza zur Winterzeit ist bemerkenswert, wenn man das Datenrauschen berücksichtigt; er zeigt, dass es möglich sein könnte, auf kurze Sicht leistungsfähige probabilistische Vorhersagen von Influenza-Epidemien zu entwickeln.
Methoden
SIRS-Modell und Methoden Die SIRS-Modellgleichungen lauten:
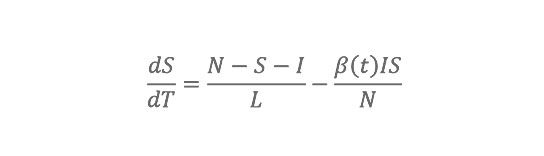
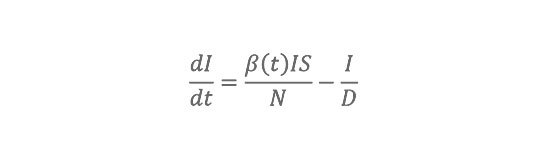
Die beobachteten Bedingungen absoluter Feuchte stammten aus einer Reanalyse der National Centers for Environmental Prediction – National Center for Atmospheric Research (NCEP-NCAR) [23]. Für jeden Staat (Arizona, Florida, Illinois, New York und Washington) wurde eine tägliche Zeitreihe von 1972–2002 der spezifischen Luftfeuchtigkeit 2 m über dem Boden, q(t), konstruiert, indem für alle Gitterzellen ein Mittelwert mit ≥ 10% der Fläche innerhalb des jeweiligen Staats gebildet wurde. Die Gleichung, die q(t) mit R0(t) in Beziehung setzt, arbeitet mit einer Exponentialfunktion, die die Verhältnisse zwischen absoluter Feuchte und sowohl dem Überleben als auch der Übertragung von Influenzaviren wiedergibt, abgeleitet aus Laborexperimenten (Abbildung 1):
Beginnend im Mai wird jedes Jahr das zufällige „Seeding“ infektiöser Individuen in der Bevölkerung (repräsentativ für Einwanderung/Reisen) auf den als dominant erfassten Subtyp für die USA festgelegt (entweder A-H1N1/B oder A-H3N2), basierend auf Labor- und Antigen-Überwachungsdaten der Centers for Disease Control/Morbidity und des Mortality Weekly Report (CDC/MMWR) [3,4]. An jedem Standort wurden fünftausend Simulationen unter Verwendung der vier Modellparameter durchgeführt: R0max, R0min, D und L wurden mittels einer Latin-Hypercube-Sampling-Struktur mit Gleichverteilung ausgewählt. Die Wertebereiche dieser Parameter wurden so festgesetzt, dass sie die bekannte Dynamik der Influenza reflektieren (siehe Tabelle S4, Text S1). Schätzwerte für R0, wie sie von vielen Autoren abgeleitet oder verwendet werden, rangieren zwischen 1,3 und 3 [16,21,22,24–27]. Um dieses Spektrum unter Berücksichtigung von Gleichung 3 und Variationen von q(t) zu erreichen, haben wir mit einer R0max zwischen 1,3 und 4 gearbeitet.
R0min gibt den Wert für R0 an, den das Modell nicht unterschreiten kann. Dieses Minimum deutet an, dass andere Übertragungswege für Influenza existieren, welche möglicherweise nicht durch die absolute Luftfeuchtigkeit moduliert werden. Werte für R0min rangieren zwischen 0,8 und 1,3. Gemäß Gleichung 4 wächst R0(t) mit abnehmender Luftfeuchtigkeit. Der Wertebereich dieses nichtlinearen Wachstums ist durch die zufällig gewählten Parameter R0max und R0min festgelegt. Schätzungen für D rangieren von 2 bis 7 Tage [16,25], Schätzungen für L von 2 bis 10 Jahre. In jeder Simulation nutzten beide Influenza-Subtypen die gleichen vier zufällig ausgewählten Parameter; die Ergebnisse waren jedoch vergleichbar, wenn jedem Subtyp andere Parameter zugewiesen wurden (insgesamt acht). Die Qualität jeder Simulation an jedem Standort wurde basierend auf dem RMS-Fehler mit beobachteter übermäßiger P&I-Sterblichkeit ausgewertet [3,4] (Abbildung S1), verzögert um zwei Wochen. Die Verzögerung simuliert die durchschnittliche Dauer von der Infektion bis zum Tod. Vor der Bestimmung des RMS-Fehlers wurde jeder Modelldurchlauf skaliert, um einen Vergleich der simulierten Infektionen mit beobachteten Sterblichkeitsraten zu ermöglichen (siehe Text S1).
Vor der Kreuzvalidierung des Modells in den zusammenhängenden USA haben wir zunächst den Effekt untersucht, den Zufälligkeit in jeder SIRS-Simulation auf die Qualität der Übereinstimmung mit Beobachtungsdaten hat. Dazu führten wir die zehn besten Common-Fit-Parameterkombinationen jeweils 100-mal für New York durch, jedes Mal mit einem anderen zufälligen Seeding. Die Korrelationen mit der beobachteten P&I-Sterblichkeit rangierten von r = 0,65 bis r = 0,97 mit einem Durchschnitt von r = 0,87. Dagegen ergab die Untersuchung mehrerer Simulationen mit der 4500-besten Parameterkombination (von 5000) Korrelationen zwischen r = -0,18 bis r = 0,34. Folglich generiert zufälliges Seeding innerhalb eines bestimmten Modelldurchlaufs ein Spektrum von Korrelationskoeffizienten; gute Modelldurchläufe sollten jedoch hohe positive Korrelationen mit Beobachtungsdaten aufweisen (im Durchschnitt r > 0,7, mindestens r > 0,5).
Dr. med. Walter J. Hugentobler
Diese Studie zeigt, dass eine niedrige absolute Luftfeuchtigkeit im Freien ein verlässlicher Prognoseparameter für den Beginn saisonaler Influenza-Epidemien ist.
Da jedoch ein direkter oder indirekter Kontakt, physisch oder durch „gemeinsam genutzte Luft“, eine unabdingbare Voraussetzung für jede mikrobielle Übertragung ist und dies größtenteils in Innenräumen geschieht, ergibt sich daraus, dass die Luftfeuchtigkeit in den Innenräumen für die Ausbreitung der Grippe entscheidend ist und nicht die absolute Feuchtigkeit der Aussenluft. Wenn Außenluft mit niedriger absoluter Luftfeuchtigkeit in Innenräume gebracht und erwärmt wird, sinkt die relative Luftfeuchtigkeit in den Innenräumen.
Wir können nichts gegen niedrige Luftfeuchtigkeit im Freien tun, aber wir können den Feuchtigkeitsgehalt der Luft in Gebäuden durch den Einsatz hygienischer Befeuchtungssysteme beeinflussen. Würden alle Gebäude eine ideale Luftfeuchtigkeit aufweisen, würden Grippeepidemien sehr begrenzt auftreten, wenn nicht sogar beseitigt. Die Grippe und die Erkältungen würden von den saisonalen Schwankungen der Außenluft abgekoppelt.
Quellen
Originaltitel: Absolute humidity and the seasonal onset of influenza in the continental United States
Quellenlink: http://dx.plos.org/10.1371/journal.pbio.10003165
Veröffentlicht:23.02.2010
1. Reichert TA, Simonsen L, Sharma A, Pardo SA, Fedson DS, et al. (2004) Influenza and the winter increase in mortality in the United States, 1959–1999. Am J Epidemiology 160: 492–502.
2. Smith DJ, Lapedes AS, de Jong JC, Bestebroer TM, Rimmelzwaan GF, et al. (2004) Mapping the antigenic and genetic evolution of influenza virus. Science 305: 371–376.
3. Simonsen L, Reichert TA, Viboud C, Blackwelder WC, Taylor RJ, et al. (2005) Impact of influenza vaccination on seasonal mortality in the US elderly population. Arch Intern Med 165: 265–272.
4. Viboud C, Bjørnstad ON, Smith DL, Simonsen L, Miller MA, et al. (2006) Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312: 447–451.
5. Centers for Disease Control and Prevention (2009) Influenza. CDC Web site. Available: http://www.cdc.gov/flu/. Accessed July 15, 2009.
6. Gething MJ, Bye J, Skehel J, Waterfield M (1980) Cloning and DNA sequence of double-stranded copies of haemagglutinin genes from H2 and H3 strains elucidates antigenic shift and drift in human influenza virus. Nature 287: 301–306.
7. Fang R, Jou WM, Huylebroeck D, Devos R, Fiers W (1981) Complete structure of A/duck/Ukraine/63 influenza hemagglutinin gene: animal virus as progenitor of human H3 Hong Kong 1968 influenza hemagglutinin. Cell 25: 315–323.
8. Smith GJD, Vijaykrishna D, Bahl J, Lycett SJ, Worobey M, et al. (2009) Origins and evolutionary genomics of the 2009 swine-origin H1N1 influenza A epidemic. Nature 459: 1122–1125.
9. Miller MA, Viboud C, Balinska M, Simonsen L (2009) The signature features of influenza pandemics—implications for policy. New Engl J Med 360: 2595–2598.
10. Lipsitch M, Viboud C (2009) Influenza seasonality: lifting the fog. Proc Natl Acad Sci U S A 106: 3645–3646.
11. Shaman J, Kohn MA (2009) Absolute humidity modulates influenza survival, transmission and seasonality. Proc Natl Acad Sci U S A 106: 3243–3248.
12. Cannell JJ, Vieth R, Umhau JC, Holick MF, Grant WB, et al. (2006) Epidemic influenza and vitamin D. Epidemiol Infect 134: 1129–1140.
13. Cannell JJ, Zasloff M, Garland CF, Scragg R, Giovannucci E (2008) On the epidemiology of influenza. Virol J 5: 29.
14. Lowen AC, Mubareka S, Steel J, Palese P (2007) Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog 3: e151. doi:10.1371/journal.ppat.0030151.
15. Lowen AC, Steel J, Mubareka S, Palese P (2008) High temperature (30uC) blocks aerosol but not contact transmission of influenza virus. J Virology 82: 5650–5652.
16. Mills CE, Robins JM, Lipsitch M (2004) Transmissibility of 1918 pandemic influenza. Nature 432: 904–906.
17. Brundage JF, Shanks GD (2008) Deaths from bacterial pneumonia during 1918– 19 influenza pandemic. Emerg Infect Dis 14: 1193–1199.
18. Ho YC, Wang JL, Wang JT, Wu UI, Chang CW, et al. (2009) Prognostic factors for fatal adult influenza pneumonia. J Infection 58: 439–445.
19. Cauchemez S, Valleron AJ, Boelle PY, Flahault A, Ferguson NM (2008) Estimating the impact of school closure on influenza transmission from Sentinel data. Nature 452: 750–754.
20. Cauchemez S, Ferguson NM, Wachtel C, Tegnell A, Saour G, et al. (2009) Closure of schools during an influenza pandemic. Lancet Inf Dis 9: 473–481.
21. Ferguson N, Cummings DAT, Cauchemez S, Fraser C, Riley S, et al. (2005) Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 437: 209–214.
22. Ferguson N, Cummings DAT, Fraser C, Cajka JC, Cooley PC, et al. (2006) Strategies for mitigating an influenza pandemic. Nature 442: 448–452.
23. Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, et al. (1996) NCEP/ NCAR 40-year reanalysis project. Bull Amer Met Soc 77: 437–471.
24. Longini IM, Halloran ME, Nizam A, Yang Y (2004) Containing pandemic influenza with antiviral agents. Am J Epidemiol 159: 623–633.
25. Longini IM Jr, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, et al. (2005) Containing pandemic influenza at the source. Science 309: 1083–1087.
26. Gani R, Hughes H, Fleming D, Griffin T, Medlock J, et al. (2005) Potential impact of antiviral drug use during influenza pandemic. Emerg Infect Dis 11: 1355–1362.
27. Germann TC, Kadau K, Longini IM, Macken CA (2006) Mitigation strategies for pandemic influenza in the United States. Proc Natl Acad Sci U S A 103: 5935–5940.
28. Harper GJ (1961) Airborne micro-organisms: survival tests with four viruses. J Hygiene 59: 479–486.
Studie Ajit Ahlawat
Die Übertragung des schweren akuten respiratorischen Syndroms Coronavirus 2 (SARS-CoV-2) durch die Luft wurde als potenzielle Pandemieherausforderung...
Einfluss der Luftfeuchte auf Mensch und Gesundheit
In der wissenschaftlichen Literatur werden unterschiedliche Empfehlungen für untere und obere Grenzwerte der relativen Luftfeuchte für Innenräume gen...
Auswirkungen von Umweltfaktoren auf COVID-19
Auswirkungen von Umweltfaktoren auf den Schweregrad und die Sterblichkeitsquote von COVID-19.
Saisonalität der respiratorischen viralen Infektionen
Der saisonale Zyklus von respiratorischen Virusinfektionen ist seit Tausenden von Jahren bekannt. Jahr für Jahr wird die Bevölkerung der gemäßigten K...
Luftfeuchtigkeit in Schulklassen
Influenza ist ein globales Problem und betrifft jährlich 5–10 % der Erwachsenen und 20–30 % der Kinder. Nicht-pharmazeutische Interventionen (NPIs) s...
COVID-19: Reduzierung der Übertragung
Aufgrund der weltweit zunehmenden Infektionen mit dem schweren akuten respiratorischen Coronavirus-2-Syndrom (SARS-CoV-2), das die Coronavirus-Krankh...
Überlebensfähigkeit von Coronaviren
In dieser Studie wurden die Auswirkungen der Lufttemperatur und der relativen Luftfeuchtigkeit auf das Überleben von Coronaviren auf Oberflächen unte...
Optimale Raumluftfeuchte
Optimale Luftfeuchte in Räumen ist notwendig, um das Wohlbefinden des Menschen zu steigern, aber im Gegensatz zu den meisten anderen Schadstoffen in ...
Auswirkung auf das Sick-Building-Syndrom
Das Ziel dieser Studie war die wissenschaftliche Auseinandersetzung der Auswirkungen von Dampfluftbefeuchtung auf das Sick-Building-Syndroms (SBS) un...
Luftfeuchtigkeit in geschlossenen Räumen
Die Studie beschäftigt sich mit direkten und indirekten Auswirkungen der relativen Luftfeuchtigkeit auf die menschliche Gesundheit.